(문제보기)
택시 기하학 성공스페셜 저지출처다국어분류
한국어
시간 제한메모리 제한제출정답맞은 사람정답 비율| 1 초 | 128 MB | 25522 | 10219 | 8800 | 39.552% |
문제
19세기 독일 수학자 헤르만 민코프스키는 비유클리드 기하학 중 택시 기하학을 고안했다.
택시 기하학에서 두 점 T1(x1,y1), T2(x2,y2) 사이의 거리는 다음과 같이 구할 수 있다.
D(T1,T2) = |x1-x2| + |y1-y2|
두 점 사이의 거리를 제외한 나머지 정의는 유클리드 기하학에서의 정의와 같다.
따라서 택시 기하학에서 원의 정의는 유클리드 기하학에서 원의 정의와 같다.
원: 평면 상의 어떤 점에서 거리가 일정한 점들의 집합
반지름 R이 주어졌을 때, 유클리드 기하학에서 원의 넓이와, 택시 기하학에서 원의 넓이를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 반지름 R이 주어진다. R은 10,000보다 작거나 같은 자연수이다.
출력
첫째 줄에는 유클리드 기하학에서 반지름이 R인 원의 넓이를, 둘째 줄에는 택시 기하학에서 반지름이 R인 원의 넓이를 출력한다. 정답과의 오차는 0.0001까지 허용한다.
예제 입력 1 복사
1
예제 출력 1 복사
3.141593 2.000000
예제 입력 2 복사
21
예제 출력 2 복사
1385.442360 882.000000
예제 입력 3 복사
42
예제 출력 3 복사
5541.769441 3528.000000
1. 문제 분석
사실 수학 파트는 어려운 문제가 없어서 풀기만하고 포스팅은 하지 않으려고 했는데 재미있는 문제가 있어서 가지고왔다.
두 점 사이의 거리를 문제에서는 다음과 같이 정의한다.
- D(T1,T2) = |x1-x2| + |y1-y2|
이 외에는 유클리드 기하학 즉, 우리가 알고있는 x, y축의 평면과 동일한 조건이다.
여기서 반지름 R이 주어졌을 때 유클리드 기하학에서의 원의 넓이와 택시 기하학에서의 원의 넓이를 구하는 문제이다.

대강 r=1 에서의 택시 기하학의 원을 그려보면 다음과 같아진다.
택시 기하학에서의 원은 한가지만 생각하면 된다.
x와 y 각각의 차이의 절댓값을 더한 값이 일정해야한다.
위의 조건을 쉽게 만드려면 (0, 0)을 중심으로 생각하고 x, y 좌표를 절대값 취해서 더해준 값이 일정해야한다는 뜻이 된다.
따라서 각 사분면마다의 간단한 일차방정식이 만들어지고(x, y절대값 합이 반지름 값이되도록 서로 일정하게 반비례하기 때문에) 결국에는 마름모 모양의 도형이 생겨나게 되는데 이가 택시 기하학에서의 원의 모양이다.
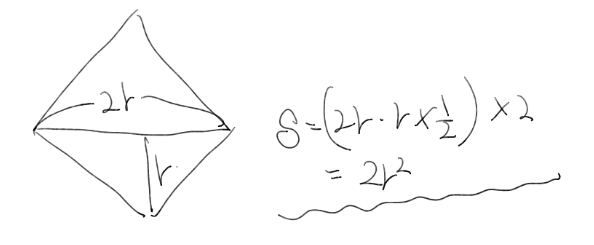
결국 위의 모양이 택시 기하학에서의 원이 되는것이고 이렇게 되면 문제는 매우 간단해진다.
원의 넓이와 마름모의 넓이를 출력하면 되는 문제가 된다.
2. 소스코드
#include<iostream>
#include<math.h>
#define PI 3.14159265359
using namespace std;
int main(void) {
double r;
cin >> r;
double pow_r = pow(r, 2);
printf("%.6lf\n%.6lf\n", pow_r * PI, pow_r * 2);
return 0;
}
주의할 점은 PI의 값을 조금 정확하게 넣어줘야한다.
정답과의 오차는 0.0001까지 허용하고, 근사값을 구하는 소수 연산인 만큼 값의 설정을 정학하게 해줘야하는 모양이다.
처음에 3.14를 넣었는데 틀리길래 바로 PI를 좀더 길게 나열했더니 맞았다.
'백준 온라인 저지 - 단계별로 풀어보기 > 기본 수학2' 카테고리의 다른 글
| 1929 - 소수 구하기 (0) | 2021.01.08 |
|---|---|
| 11653 - 소인수분해 (0) | 2021.01.08 |
| 2581 - 소수 (0) | 2021.01.08 |
| 1978 - 소수 찾기 (0) | 2021.01.08 |